ココリサーチ株式会社　ペリオマチックとは

技術情報　ペリオマチック^TMとは

ペリオマチック^TMとは
ココリサーチが世界に先がけ独自開発した、周期方式の周波数計測技術です。
・ダイナミック予測^TM（双曲線予測演算）や停止予測も装備し、
・動き出しや停止、超低速から高速、急加速・急停止などの変化まで
・あらゆる状況下で高精度・高速応答を実現します。

過去の回転速度計測：周波数から測る
ゲート時間内のパルス数を数えて、応答します。

周波数から測る方法の問題点
低速の場合：
■ゲート時間よりも速い応答は不可能
■ゲート時間を短くすると1ビットエラーの影響が増し、計測精度が下がります
■アナログ出力を得るときにも、波ごとにリップル障害が発生します

例：パルスごとの応答ができない

これ以降パルスが入らないのに、ゲート締切まで待たないといけません。

例：1ビットエラーとリップル障害

リップル障害：波形の乱れをリップルといいます。
一定周期のパルス入力でも、ゲート締切のタイミング次第で、出力が乱れます。

低速回転の例
■風車の低速回転

回っているのに、出力は0になってしまっています。

■シールドマシン
- 機長：約9m
- 総重量：約600t
- 掘削速度：1日あたり約7.5m (本掘進時)

回転速度を測れないと、2台のシールドマシンが合流しません。

ペリオマチックは周期（Period）から測ります
■2パルスの入力で周期がわかり、1ビットエラーの影響がありません
■リップル障害がありません

ペリオマチックで、過去の測定方法の問題を解決

従来のゲート方式	ペリオマチック方式
ゲート時間よりも速い応答は不可	1周期ごとに応答可能
ゲート時間が短いと1ビットエラーの影響が大きくなり、計測精度が下がる	2パルスの入力で周期がわかるため、1ビットエラーの影響がない
アナログ出力を得るときにも、波ごとにリップル障害が発生	リップル障害がない

周波数と周期の関係
入力周波数が低下すると、 1パルス前の周期より周期が延びます。
　　▼
前の周期と比べ、計測出力は小さくなります。
　　▼
ペリオマチックの予測演算は、直角双曲線を演算しながら計測出力を下げます。

周波数と周期は、逆数関係なのでｆ＝1/T

直角座標上で、直角双曲線になります。

ペリオマチック^TMA方式の動作例
パルス入力と、ペリオマチック^TMA方式の演算によるF/V電圧出力は、このようになります。
ピンク色部分が、ダイナミック予測^TMの有無による違いです。
計測結果に大きく違いが出ています。
＊ペリオマチック^TMB方式にもダイナミック予測^TM機能があり、ゲート時間ごとに更新されます。

ペリオマチック^TMB方式について
パルス信号と出力更新時間を内部ゲートとして、
その間の入力パルス数を計測
　　▼
パルス数と同時にパルスの周期を計測し
周期の合計値を求めて平均化する
　　▼
周期の合計値をパルス数で割る
　　▼
1パルスあたりの平均周期の計測が可能

ペリオマチック^TMBの動作例：従来のゲート方式と比較

例1：ゲート時間1ms、入力パルス1.5kHzの場合

例2：入力周波数に変動がある場合

まとめ：ペリオマチック^TMA方式・B方式
ペリオマチック^TMには、A方式（応答優先）とB方式（精度優先）があります。

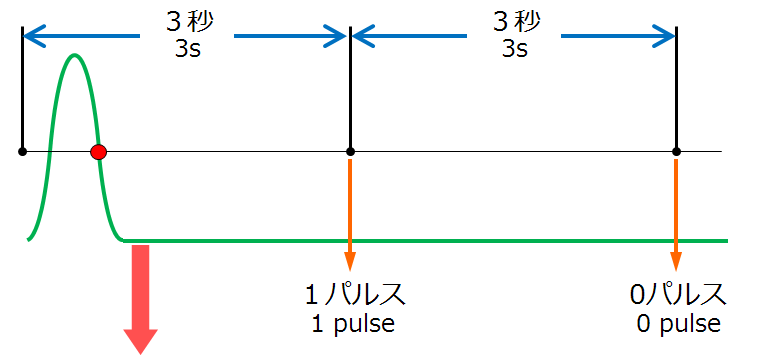
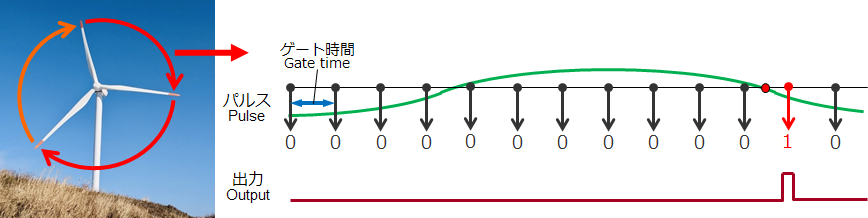
ペリオマチック^TMA：独自の1パルス応答

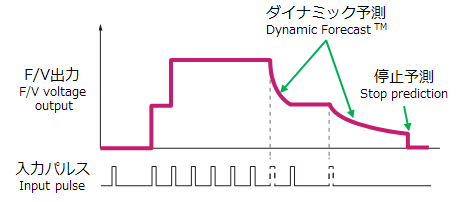
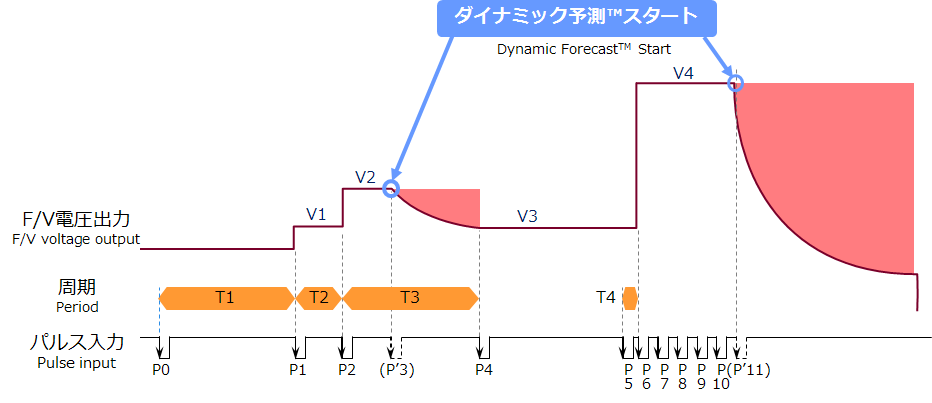
■高速応答（1パルス応答が可能）
■加速時：1パルス応答で高速応答、急加速も高精度で追従
■減速時：ダイナミック予測(双曲線予測演算)で正確な予測演算
■停止時：使用状況に応じた適宜なタイミングで停止予測

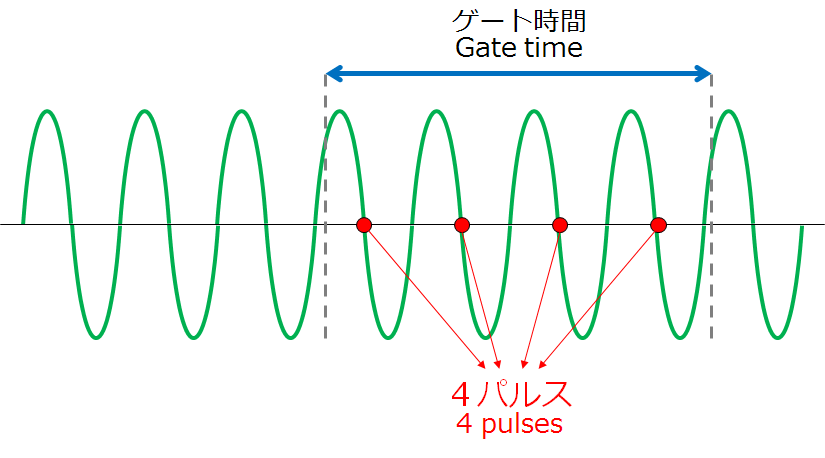
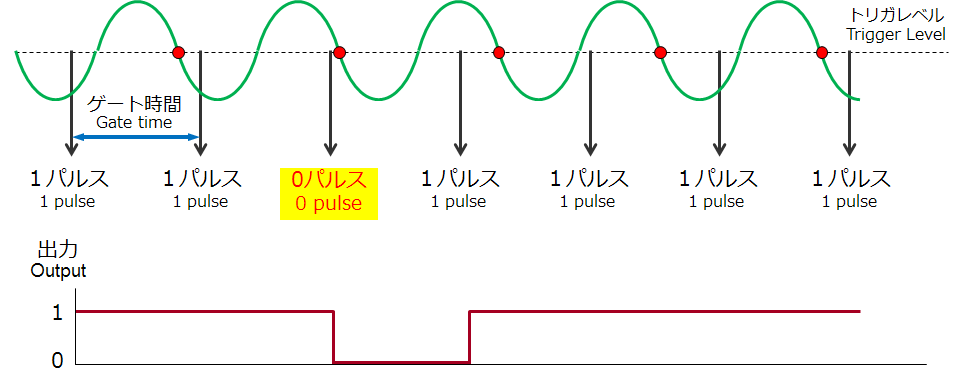
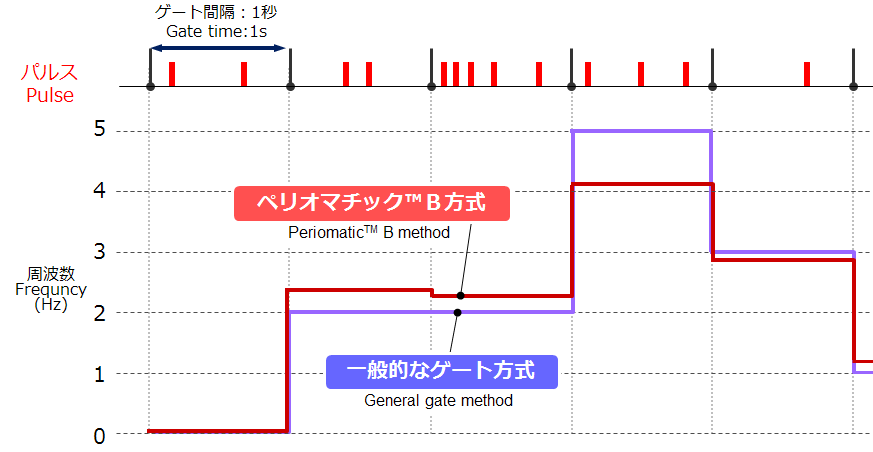
ペリオマチック^TMB：独自のゲート方式

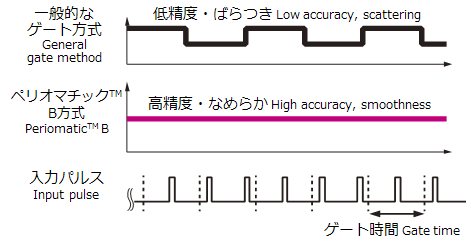
■時間平均
■短いゲート期間でも、高精度が得られる
■ゲート時間内のパルス数と周期を精密に測り、平均化
■一般的なゲート方式で起こるゲート時間内のパルス数エラーがなく、パルスのムラなどに強い
■減速時は予測演算も働き、高精度・高速応答

A方式・B方式　共通の特長
■広範囲計測（低速から高速まで）　■超低速にも強い　■高精度
ペリオマチック^TM方式によって、回転速度の詳密な計測が可能になり、ココリサーチは回転解析という言葉を提唱しました。

用途例をみる：計測・制御など

関連機種をみる

技術情報 ペリオマチックTMとは

技術情報　ペリオマチック^TMとは